Мерность восприятия. Геометрия
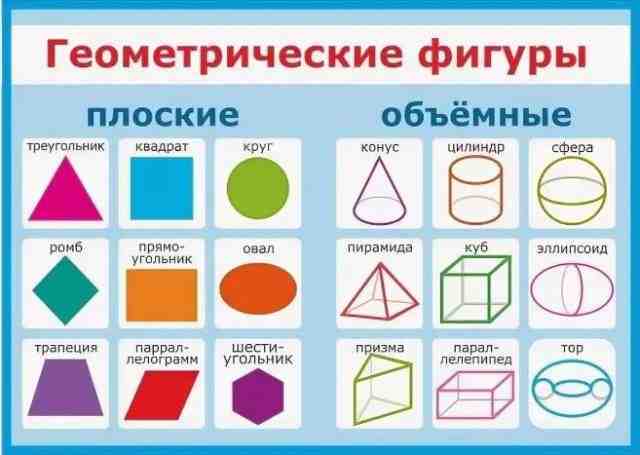
Проверим, сможете ли вы соотнести понятия геометрии: точка, линия, плоскость, куб, с понятиями алгебры и математических функций: состояние, процесс, множество процессов.
_________________________________________________________________
Знакомясь с плоскими и объемными геометрическими фигурами, мы знакомимся с геометрией и тригонометрией, а по сути, со связанными (смежными) понятиями, такими как площадь: форма, объем. Даже если вы не знакомы с алгеброй и математикой, вы легко можете проверить правильность суждения: различные объемные фигуры получаются путем вращения плоских 2-х мерных геометрических фигур вокруг своей оси. Берем 2-х мерные фигуры (треугольник, прямоугольник, круг), вращаем их и получаем 3-х мерные объемные фигуры: конус, цилиндр, шар. В зависимости от того, где находится ось вращения можно получать самые разные фигуры. Что нужно сделать с 3-х мерной фигурой, чтобы получить 4-х мерную фигуру (объект)?
В математике мы знакомимся с теорией функций. Сначала с простейшими из них, затем наступает очередь более сложных разделов математики. В алгебре мы знакомимся с теорией множеств. Попробуем соотнести простейшие понятия геометрии (фигуры различной мерности), математики (функции — абстрактные модели процессов), и алгебры, с понятиями: время (длительность процессов) и пространство (его мерность), чтобы понять кое-что про мерность нашего визуального восприятия мира.
Рис. 1. Плоские и объемные геометрические фигуры. Из плоских фигур легко получить объёмные фигуры. Главное правильно выбрать ось вращения и тип движения. Из треугольника при вращении получим конус, а при поступательном движении призму.
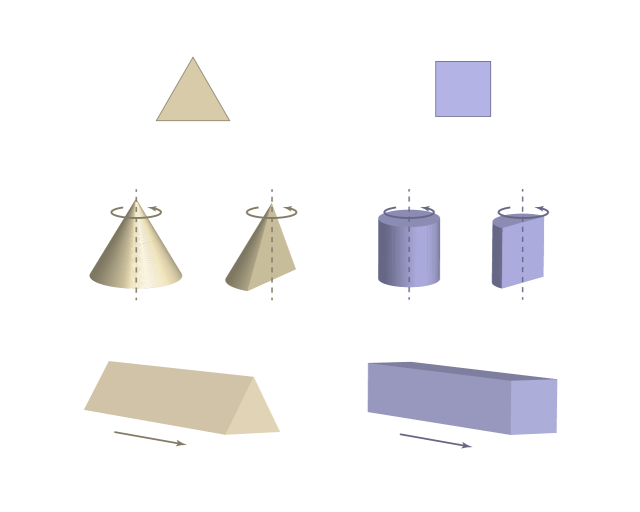
Предлагаю поразмышлять, пофантазировать, на тему: что может представлять из себя четырехмерный объект, а затем и 4-х мерное пространство. Заметьте, не пространство-время, не пространственно-временной континуум, а просто; 4-мерный объект и 4-х мерное пространство. Было предпринято множество попыток, авторы которых пытались ответить на этот вопрос, но мы пойдем своим путем.
Таблица №1
Анализ восприятия геометрических пространств
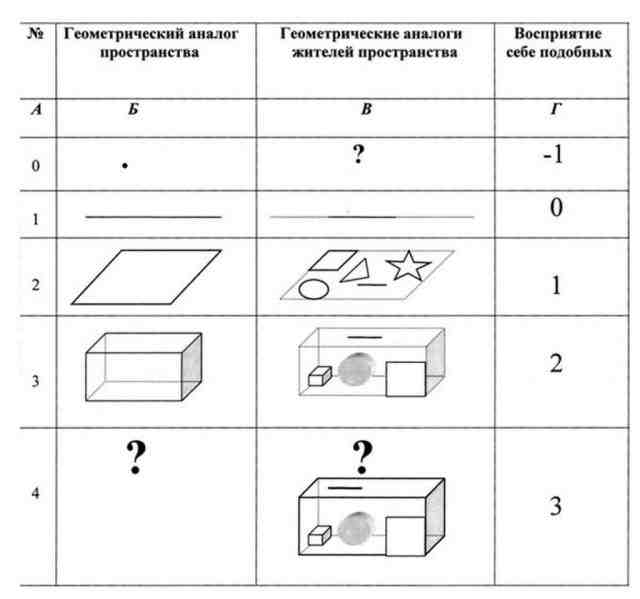
Взгляните на таблицу 1.
В столбце «А» отображена размерность пространства. В данном случае мы будем рассматривать пространства с мерностью от 0 до 4. Разберемся с 4-х мерным пространством, можно будет пойти дальше и подумать над тем, что такое 5 и 6-мерное пространство?
В столбце «Б» нашей таблицы показаны некоторые геометрические аналоги таких пространств. Аналогом 0-мерного пространства является точка, 1-мерного пространства — прямая линия, 2-мерного пространства — плоскость, 3-мерного пространства — куб, 4-мерного пространства — непонятно, знак вопроса?. Это и предстоит выяснить — что может быть геометрическим аналогом 4-мерного пространства, как оно выглядит?
В столбце «В» изображены геометрические аналоги некоторых «жителей» таких пространств. Кто живет в 0-мерном пространстве непонятно? Если я скажу: точки меньших размеров, чем та о которой идет речь, то будет непонятно, о чем, вообще, идет речь. 🙂
В 1-мерном пространстве, т.е. в линии, может «жить» бесконечное множество различных объектов: отрезки, т.е. объекты такой же мерности, но меньших размеров и объекты у которых мерность на 1 меньше, т.е. точки.
В 2-мерном пространстве могут «жить»: точки, отрезки, линии, треугольники, квадратики, круги и т.д., т.е. объекты такой же мерности, но меньших размеров, и 1-мерные и 0-мерные объекты.
В 3-мерном пространстве могут «жить»: точки, отрезки, линии, плоскости, шарики, кубики, цилиндры, конусы и т.д., т.е. объекты такой же мерности, но меньших размеров и 2, 1, 0 — мерные.
На вопрос: кто может «жить» в 4-мерном пространстве, можно ответить по аналогии. В 4-мерном пространстве могут «жить»: точки, отрезки, линии, треугольники, квадратики, круги, плоскости, шарики, кубики, цилиндры, конусы и 4-мерные объекты, но меньших размеров, а также 3, 2, 1, 0-мерные объекты.
Вывод: Пространства меньшей мерности могут быть вложенными в пространства большей мерности.
Чтобы ответить на вопрос: как могут «выглядеть» 4-мерные объекты («жители» 4-мерного пространства и само 4-мерное пространство), сначала придется придется ответить на более простой вопрос о том, как зависит мерность зрительного восприятия объектов различной мерности от мерности самого воспринимающего субъекта?
В столбце «Г», отражена мерность зрительного восприятия «себе подобных». Представим себе, навстречу друг другу в «мире», которым является прямая линия, бегут два отрезка. Допустим, что у них, даже, есть «глаза». Спрашивается — они будут видеть, что они отрезки или нет? А когда в «мире», которым является «плоскость», встречаются треугольник и квадрат, они будут видеть, что они треугольник и квадрат? А когда в нашем реальном трехмерном мире мы смотрим, друг на друга, разве мы видим то, что написано у нас на спине?
Получается, что мерность зрительного восприятия себе подобных, т.е. субъектов/объектов с такой же мерностью, на единичку меньше мерности самого объекта. Это означает, что если в «мире», которым является «плоскость», столкнутся два ее жителя, треугольник и квадрат, то они будут воспринимать друг друга с помощью зрения, как отрезки. А, если в «мире», которым является «линия», встретятся два отрезка, то они будут воспринимать друг друга с помощью зрения, как точки.
В столбце «2» отражена мерность зрительного восприятия «старшими братьями» «братьев меньших» (см. рис. ниже). Для того, чтобы понять, как получается, что мерность восприятия «старшими младших» равна мерности младших, надо представить, что вы подходите к «миру», которым является «плоскость» и наблюдаете за его жителями. В этом 2-мерном «мире» живут 0, 1, 2-мерные объекты. Что интересно, вы и видите их как 0, 1, 2-мерные объекты, т.е. в их «истинной мерности», но не забывайте, что Вы трехмерные. Аналогично, в 2-мерном мире, треугольник будет «видеть» отрезок, т.е. 1-мерный объект, который является «жителем» этого же мира, как 1-мерный объект, т.е. в его истинной мерности.
На самом деле, ситуация становится чуть сложнее, если вспомнить, что объекты могут перемещаться в мире, в котором они живут. Представим себе, что треугольник, живущий в «плоскости», наблюдая за отрезком, вдруг, увидел вместо него точку. Возможно ли такое? Конечно, если отрезок совершал вращательное движение, то в какой-то момент времени он может повернуться к наблюдателю таким образом, что тот увидит вместо отрезка точку.
Разумеется, все сказанное по отношению к столбцу «2» (см. рис ниже) справедливо только в том случае, если «мир» меньшей мерности является подмножеством вашего мира, т.е. вложен в него (является его частью). А, если ситуация иная? Например, отрезок проходит сквозь плоскость. В этом случае треугольник вместо отрезка будет видеть только точку. Ну, уж мы то, с вами будем видеть все: и то, что треугольник видит только точку, вместо отрезка, и то, что на самом деле точка является отрезком, ведь мы же трехмерные, не так ли?
В столбце «3» отражена мерность зрительного восприятия «братьями меньшими» «старших братьев» (см. рис ниже). Чтобы разобраться, чуть-чуть, как обстоят дела в этом случае, необходимо представить себе следующую ситуацию. Допустим, что на каком-то семинаре, который проходил в «2-мерном мире» (в банальной плоскости) собрались вместе: треугольник, квадрат, прямоугольник, круг и др., для того чтобы обсудить вопрос — есть ли миры высшей мерности, нежели тот, в котором живут они, и как могут выглядеть «жители» таких миров? На самом деле, их «мир» был вложен в наш, и вы имели возможность наблюдать за всем ходом такого собрания.
Таблица 2. Собрание на тему «Существуют ли пространства высшей мерности»?
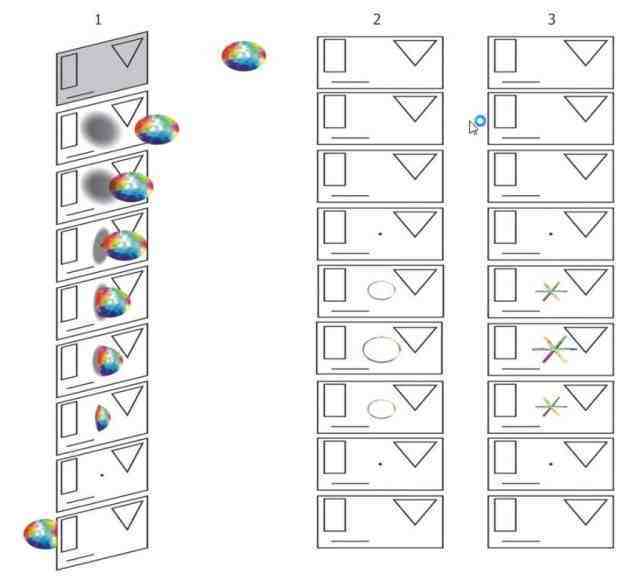
Мерность объектов и мерность восприятия
Представим себе, что вы решили в это же время изучить несколько иной вопрос: как «жители» 2-мерного мира будут воспринимать в визуальной модальности «посылки» из трехмерного мира. Для проведения эксперимента был взят резиновый глобус. Почему вы взяли не просто мяч, а глобус, вы скоро поймете. Вы поставили его на пол, разбежались и пнули, с таким расчетом, чтобы он прилетел в гости к «жителям» 2-мерного мира, у которых в это время шел семинар. Вы еще не забыли тему семинара? Как, там, у Б.Окуджавы: «…девочка плачет, а шарик летит…». В данном случае резиновый глобус летит, а они (семинаристы) и не подозревают о том, что их ждет встреча с чудом.
Допустим, что все это происходило прямо на футбольном поле: 2-мерный мир, т.е. плоскость (экран) был установлен в створе футбольных ворот, а «мяч» вы послали в гости с центра поля, причем, за спиной у вас находился мощный прожектор. Для чего нужен прожектор, вы уже поняли? Правильно, он дает тень. Напомню, тень — это то же самое, что и след, а след — это результат взаимодействия,— минимально возможная визуальная информационная копия, в данном случае, «мяча».
Понятно, что мерность тени меньше мерности самого объекта — «мяча». По мере приближения «мяча», тень будет изменяться в размерах. В том случае, если она попадает в «мир» семинаристов. она будет вносить некоторые изменения в их «МИР» — но слабые, т.е. информационные. Внимательные и чувствительные смогут обнаружить эти изменения (информацию) раньше, нежели «мяч» коснется их «мира» (до того, как взаимодействие станет сильным, т.е. энергетическим, т.е. связанным с ощущениями). В этом случае изменения произойдут, в первую очередь, в органе, который изменяется гораздо быстрее мышц, т.е. в мозге. Еще. «никто не прилетел, но изменится эмоциональное состояние.
Как же будет выглядеть результат взаимодействия «мяча» (з-х мерный объект) с 2-мерным миром (плоскость), для нас, и для участников семинара? Понятно, что если наша точка наблюдения находится за прожектором, то «мяч» заслонит для нас результат своего взаимодействия с 2-мерным миром: но если мы переместимся и займем положение так, чтобы наблюдать процесс их взаимодействия, мы увидим, что сначала это будет точка, которая превратится в круг, а затем круг, достигнув своего максимального размера, сожмется в точку и исчезнет, когда «мяч» пройдет сквозь их мир, т.е. для нас результат взаимодействия будет являться объектом, у которого мерность меняется от 0 до 2-х, а затем, обратно от 2-х до 0.
А что же увидят «жители» 2-мерного «мира», к которым в гости прилетел 3-мерный «подарок»? Сначала точку (в момент начального взаимодействия). Затем точка превратится в отрезок, размеры которого будут изменяться, от минимального до максимального, после чего отрезок будет сжиматься до размеров точки, и наконец, исчезнет совсем.
Итак, в гости прилетел 3-мерный объект, а воспринимать его жители 2-мерного мира будут, в лучшем случае, как объект с мерностью от 0 до 1. Этот вывод можно было сделать и раньше. Понятно, что при встрече объектов с разной мерностью результат их взаимодействия (след) будет меняться от 0 до мерности объекта, у которого она наименьшая. Мерность восприятия следа будет не выше мерности восприятия «себе подобных»: в 2-мерном «мире» — это 1, в 1-мерном «мире» — это 0, в 3-мерном «мире» — это 2.
Но, ситуация интересна еще и тем, что очевидцы события («треугольник», «квадрат», «прямоугольник» и «круг») увидят разные отрезки (на самом деле следы — результат взаимодействия), как по расположению в пространстве и размерам (если наш мяч-глобус сделан из резины, имеющей различную плотность), так и по «окраске», т.е. информационной насыщенности, т.к. к кому-то «мяч-глобус» будет повернут «Тихим океаном», а к кому-то «Австралией».
Товарищам-семинаристам будет очень трудно понять, откуда «прилетел» этот странный объект, куда он «улетел» (кстати, улететь он может и не туда, откуда прилетел), когда и куда он «прилетит» вновь, а главное, зачем он появлялся? Вполне возможно, не все из них поймут, что то, что они видели – не есть сам «посланец» — это только след, да и то, воспринятый не во всей своей «полноте». Нельзя ставить знак равенства между самим объектом и следом (отпечатком), то есть результатом взаимодействия!
ЧХ и длительность предъявления объекта
Существует еще несколько интересных моментов, мимо которых нельзя пройти. Допустим, что зрение жителей 2-мерного мира работает в том же амплитудно-частотном диапазоне, что и у нас с вами. Но очень многое в восприятии «гостя» будет зависеть от времени его пребывания в их 2-мерном “мире”, того с какой частотой он появляется и с какой скоростью перемещается.
Пример: если вы возьмете из костра горящий прутик, а дело будет происходить ночью, и будете вращать его с большой скоростью, то сторонний наблюдатель будет видеть не прутик, а траекторию его движения, которая может иметь достаточно сложную форму и при определенных условиях (очень большая скорость и повторяющаяся траектория) может восприниматься как некий стабильный объект. Например, результатом вращения прутика может быть окружность, овал, отрезок и т.п.
А, вспомните пресловутую историю с “25 кадром”. В данном случае время предъявления некоего объекта составляет 1/25 секунды. В этом случае подсознание фиксирует этот объект, т.к. информация через зрительный канал все-таки попадает в мозг, и выдаст на этот объект некоторую реакцию, которая будет неосознанной.
Вам хорошо известно, что частота колебаний напряжения в осветительной сети составляет 50 Гц (50 колебаний в секунду). Глаз эти колебания не воспринимает, т.к. частота колебаний (модуляций) превышает пороговую — 25 Гц.
Но вернемся к нашим испытуемым:: «кругам», «квадратам», «треугольникам», т.е. “жителям” 2-мерного “мира”, которые все еще обсуждают результат появления в их мире вашей посылки (мяча — глобуса). Они обсуждают следующие вопросы: что это было, откуда оно взялось, почему его расположение в пространстве и цвет, все видели по разному, куда подевались «треугольник» и «квадрат», которых накрыл этот объект (в случае, если мяч был «намазан чем-нибудь липким» и попал прямо в эпицентр собрания, к нему могли «прилипнуть» пара другая семинаристов и на время исчезнуть из своего «мира» совершенно непонятным для остальных образом), и почему они появились через некоторое время, но в другом месте.
Итак, они обсуждают вышеперечисленные вопросы, а вы пошли на следующий эксперимент: подошли к их “миру” и постучали по нему пальцем, затем поводили по нему пальцем, но с очень большой скоростью. А, в довершение всего, вы коснулись их “мира” всеми пальцами одновременно, затем свели их в щепотку, снова развели в стороны и, наконец, отошли в сторону, чтобы посмотреть, что будет дальше и подумать над вопросом — смогут ли они понять, что отрезки, которые они воспринимали, на самом деле являются вашими пальчиками, которые могут править их миром, как вам вздумается.
Гедель на это ответил однозначно, но не будем торопиться с выводами…


Рис. 2. Угра, 2019.06. Отличный пример на тему ограниченности нашего визуального восприятия. Одно можно сказать точно — это след. На другом снимке его уже не видно.
Автор текста: к.п.н. А.Н.Чистяков
Более подробно про восприятие процессов: https://go-ra.ru/lektsii/lecture/lec04/vp/
P.S. Сейчас в интернет вбрасывается огромное количество мусорной информации, что приводит большинство людей к клиповому мышлению и отсутствию здравомыслия. И если вы смогли прочитать статью до конца, да еще уловить её смысл, то смело переходите на сайт https://go-ra.ru Там вы найдете еще больше интересных материалов. Ознакомившись подробнее, возможно, у вас появиться желание принять участие в Проекте GO-RA.
Информация об обучении и семинарах: https://go-ra.ru/grafik-obucheniya/seminary/








